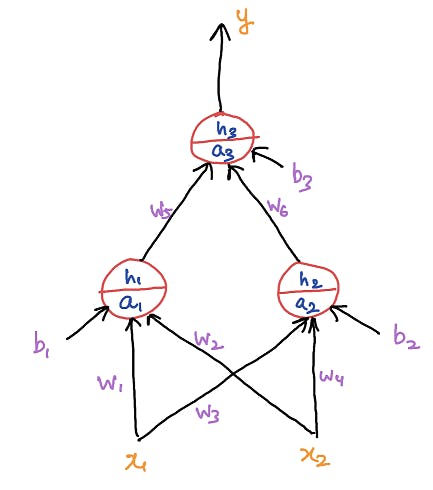
In this article, we will see in how many ways we can implement Feed Forword Neural Networks in PyTorch. For this we will be using a three neurons network that takes two input features and gives output through the last neuron as shown in fig.
Importing Libraries
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.colors
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error, log_loss
from tqdm import tqdm_notebook
import seaborn as sns
import time
from IPython.display import HTML
import warnings
warnings.filterwarnings('ignore')
from sklearn.preprocessing import OneHotEncoder
from sklearn.datasets import make_blobs
import torch
torch.manual_seed(0)
<torch._C.Generator at 0x7fe9c97a04d0>
my_cmap = matplotlib.colors.LinearSegmentedColormap.from_list("", ["red","yellow","green"])
Generate Dataset
data, labels = make_blobs(n_samples=1000, centers=4, n_features=2, random_state=0)
print(data.shape, labels.shape)
(1000, 2) (1000,)
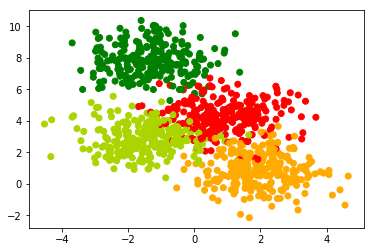
plt.scatter(data[:,0], data[:,1], c=labels, cmap=my_cmap)
plt.show()
X_train, X_val, Y_train, Y_val = train_test_split(data, labels, stratify=labels, random_state=0)
print(X_train.shape, X_val.shape, labels.shape)
(750, 2) (250, 2) (1000,)
Using torch tensors and autograd
X_train, Y_train, X_val, Y_val = map(torch.tensor, (X_train, Y_train, X_val, Y_val))
print(X_train.shape, Y_train.shape)
torch.Size([750, 2]) torch.Size([750])
def model(x):
a1 = torch.matmul(x, weights1) + bias1 # (N, 2) x (2, 2) -> (N, 2)
h1 = a1.sigmoid() # (N, 2)
a2 = torch.matmul(h1, weights2) + bias2 # (N, 2) x (2, 4) -> (N, 4)
h2 = a2.exp()/a2.exp().sum(-1).unsqueeze(-1) # (N, 4)
return h2
y_hat = torch.tensor([[0.1, 0.2, 0.3, 0.4], [0.8, 0.1, 0.05, 0.05]])
y = torch.tensor([2, 0])
(-y_hat[range(y_hat.shape[0]), y].log()).mean().item()
(torch.argmax(y_hat, dim=1) == y).float().mean().item()
0.5
def loss_fn(y_hat, y):
return -(y_hat[range(y.shape[0]), y].log()).mean()
def accuracy(y_hat, y):
pred = torch.argmax(y_hat, dim=1)
return (pred == y).float().mean()
torch.manual_seed(0)
weights1 = torch.randn(2, 2) / math.sqrt(2)
weights1.requires_grad_()
bias1 = torch.zeros(2, requires_grad=True)
weights2 = torch.randn(2, 4) / math.sqrt(2)
weights2.requires_grad_()
bias2 = torch.zeros(4, requires_grad=True)
learning_rate = 0.2
epochs = 10000
X_train = X_train.float()
Y_train = Y_train.long()
loss_arr = []
acc_arr = []
for epoch in range(epochs):
y_hat = model(X_train)
loss = loss_fn(y_hat, Y_train)
loss.backward()
loss_arr.append(loss.item())
acc_arr.append(accuracy(y_hat, Y_train))
with torch.no_grad():
weights1 -= weights1.grad * learning_rate
bias1 -= bias1.grad * learning_rate
weights2 -= weights2.grad * learning_rate
bias2 -= bias2.grad * learning_rate
weights1.grad.zero_()
bias1.grad.zero_()
weights2.grad.zero_()
bias2.grad.zero_()
plt.plot(loss_arr, 'r-')
plt.plot(acc_arr, 'b-')
plt.show()
print('Loss before training', loss_arr[0])
print('Loss after training', loss_arr[-1])
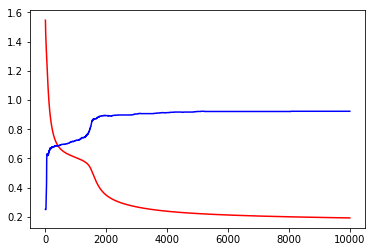
Loss before training 1.5456441640853882
Loss after training 0.19288592040538788
Using NN.Functional
import torch.nn.functional as F
torch.manual_seed(0)
weights1 = torch.randn(2, 2) / math.sqrt(2)
weights1.requires_grad_()
bias1 = torch.zeros(2, requires_grad=True)
weights2 = torch.randn(2, 4) / math.sqrt(2)
weights2.requires_grad_()
bias2 = torch.zeros(4, requires_grad=True)
learning_rate = 0.2
epochs = 10000
loss_arr = []
acc_arr = []
for epoch in range(epochs):
y_hat = model(X_train)
loss = F.cross_entropy(y_hat, Y_train)
loss.backward()
loss_arr.append(loss.item())
acc_arr.append(accuracy(y_hat, Y_train))
with torch.no_grad():
weights1 -= weights1.grad * learning_rate
bias1 -= bias1.grad * learning_rate
weights2 -= weights2.grad * learning_rate
bias2 -= bias2.grad * learning_rate
weights1.grad.zero_()
bias1.grad.zero_()
weights2.grad.zero_()
bias2.grad.zero_()
plt.plot(loss_arr, 'r-')
plt.plot(acc_arr, 'b-')
plt.show()
print('Loss before training', loss_arr[0])
print('Loss after training', loss_arr[-1])
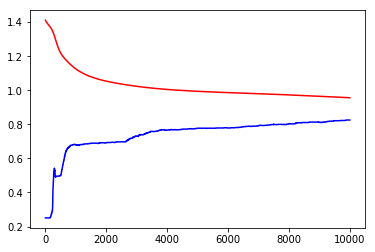
Loss before training 1.4111980199813843
Loss after training 0.9561842679977417
Using NN.Parameter
import torch.nn as nn
class FirstNetwork(nn.Module):
def __init__(self):
super().__init__()
torch.manual_seed(0)
self.weights1 = nn.Parameter(torch.randn(2, 2) / math.sqrt(2))
self.bias1 = nn.Parameter(torch.zeros(2))
self.weights2 = nn.Parameter(torch.randn(2, 4) / math.sqrt(2))
self.bias2 = nn.Parameter(torch.zeros(4))
def forward(self, X):
a1 = torch.matmul(X, self.weights1) + self.bias1
h1 = a1.sigmoid()
a2 = torch.matmul(h1, self.weights2) + self.bias2
h2 = a2.exp()/a2.exp().sum(-1).unsqueeze(-1)
return h2
def fit(epochs = 1000, learning_rate = 1):
loss_arr = []
acc_arr = []
for epoch in range(epochs):
y_hat = fn(X_train)
loss = F.cross_entropy(y_hat, Y_train)
loss_arr.append(loss.item())
acc_arr.append(accuracy(y_hat, Y_train))
loss.backward()
with torch.no_grad():
for param in fn.parameters():
param -= learning_rate * param.grad
fn.zero_grad()
plt.plot(loss_arr, 'r-')
plt.plot(acc_arr, 'b-')
plt.show()
print('Loss before training', loss_arr[0])
print('Loss after training', loss_arr[-1])
fn = FirstNetwork()
fit()
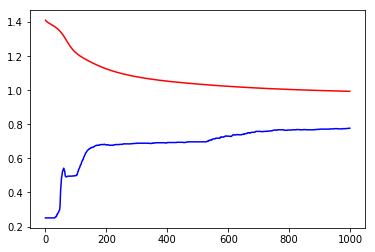
Loss before training 1.4111980199813843
Loss after training 0.9939236640930176
Using NN.Linear and Optim
class FirstNetwork_v1(nn.Module):
def __init__(self):
super().__init__()
torch.manual_seed(0)
self.lin1 = nn.Linear(2, 2)
self.lin2 = nn.Linear(2, 4)
def forward(self, X):
a1 = self.lin1(X)
h1 = a1.sigmoid()
a2 = self.lin2(h1)
h2 = a2.exp()/a2.exp().sum(-1).unsqueeze(-1)
return h2
fn = FirstNetwork_v1()
fit()
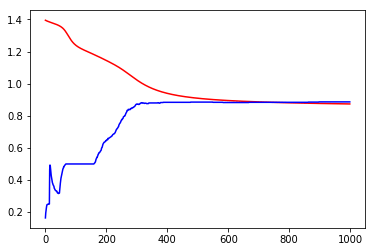
Loss before training 1.395160436630249
Loss after training 0.8738410472869873
from torch import optim
def fit_v1(epochs = 1000, learning_rate = 1):
loss_arr = []
acc_arr = []
opt = optim.SGD(fn.parameters(), lr=learning_rate)
for epoch in range(epochs):
y_hat = fn(X_train)
loss = F.cross_entropy(y_hat, Y_train)
loss_arr.append(loss.item())
acc_arr.append(accuracy(y_hat, Y_train))
loss.backward()
opt.step()
opt.zero_grad()
plt.plot(loss_arr, 'r-')
plt.plot(acc_arr, 'b-')
plt.show()
print('Loss before training', loss_arr[0])
print('Loss after training', loss_arr[-1])
fn = FirstNetwork_v1()
fit_v1()
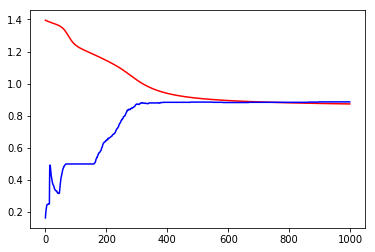
Loss before training 1.395160436630249
Loss after training 0.8738410472869873
Using NN.Sequential
class FirstNetwork_v2(nn.Module):
def __init__(self):
super().__init__()
torch.manual_seed(0)
self.net = nn.Sequential(
nn.Linear(2, 2),
nn.Sigmoid(),
nn.Linear(2, 4),
nn.Softmax()
)
def forward(self, X):
return self.net(X)
fn = FirstNetwork_v2()
fit_v1()
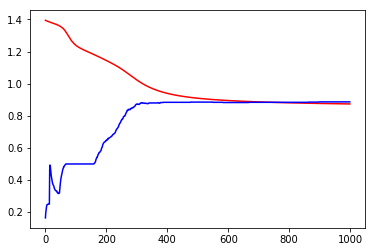
Loss before training 1.395160436630249
Loss after training 0.8738410472869873
def fit_v2(x, y, model, opt, loss_fn, epochs = 1000):
for epoch in range(epochs):
loss = loss_fn(model(x), y)
loss.backward()
opt.step()
opt.zero_grad()
return loss.item()
fn = FirstNetwork_v2()
loss_fn = F.cross_entropy
opt = optim.SGD(fn.parameters(), lr=1)
fit_v2(X_train, Y_train, fn, opt, loss_fn)
0.8738410472869873
Running it on GPUs
device = torch.device("cuda")
X_train=X_train.to(device)
Y_train=Y_train.to(device)
fn = FirstNetwork_v2()
fn.to(device)
tic = time.time()
print('Final loss', fit_v2(X_train, Y_train, fn, opt, loss_fn))
toc = time.time()
print('Time taken', toc - tic)
Final loss 1.395159363746643
Time taken 0.7891602516174316
class FirstNetwork_v3(nn.Module):
def __init__(self):
super().__init__()
torch.manual_seed(0)
self.net = nn.Sequential(
nn.Linear(2, 1024*4),
nn.Sigmoid(),
nn.Linear(1024*4, 4),
nn.Softmax()
)
def forward(self, X):
return self.net(X)
device = torch.device("cpu")
X_train=X_train.to(device)
Y_train=Y_train.to(device)
fn = FirstNetwork_v3()
fn.to(device)
tic = time.time()
print('Final loss', fit_v2(X_train, Y_train, fn, opt, loss_fn))
toc = time.time()
print('Time taken', toc - tic)
Final loss 1.3890225887298584
Time taken 29.352728128433228
Thanks for reading :)